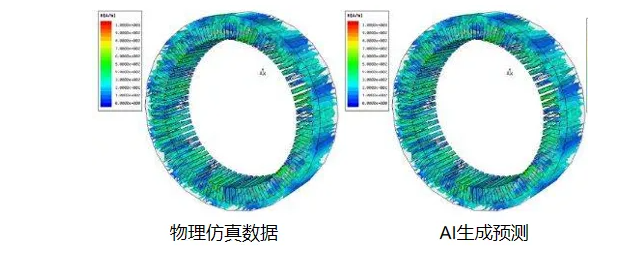
贝叶斯优化(Bayesian Optimization)作为一种高效的全局优化方法,在复杂设计空间探索和多目标优化中展现了强大的能力。结合生成模型,贝叶斯优化能够显著提升CAE仿真中的拓扑优化效率。本文将重点介绍贝叶斯优化的多种技术,包括高斯过程、核回归、贝叶斯神经网络等,以及它们在轻量化和强度优化中的应用场景。
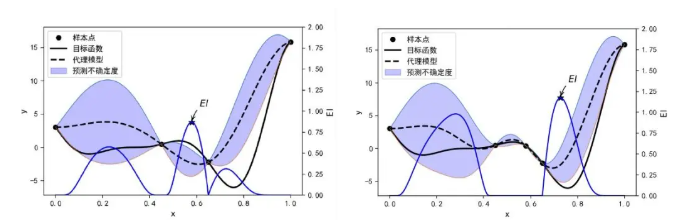
高斯过程(Gaussian Process, GP)GP 是贝叶斯优化中最常用的模型,用于构建代理模型并提供不确定性度量。在 CAE 仿真中,GP 可以作为生成模型的代理,用于优化结构参数(如材料分布或几何形状),平衡轻量化与强度。通过采样少量点建立代理模型,GP 可在生成初始拓扑结构的基础上找到最优设计方案。
核回归通过核函数计算点之间的相似性,以估计未知设计空间的目标函数。核回归在多目标优化中适合生成具有相似拓扑特征的结构,结合生成模型生成初始结构后,可以利用核回归优化设计参数,找到满足轻量化和强度要求的最优设计。核嵌入高斯过程(Gaussian Process with Kernels, GP-Kernel)GP-Kernel 结合不同的核函数(如 RBF、Matern 核)来提高代理模型的表达能力。在 CAE 仿真中,GP-Kernel 可以用于复杂拓扑结构的多目标优化,尤其适合生成模型初步生成的高维设计空间。结合强化学习算法,GP-Kernel 可以高效搜索不同拓扑结构组合,使设计符合轻量化和强度等多个目标需求。
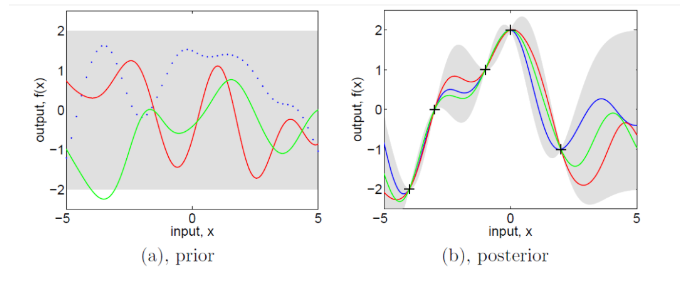
贝叶斯神经网络(Bayesian Neural Network, BNN)BNN 使用贝叶斯方法对神经网络的权重进行建模,能够处理高维复杂的设计空间。在 CAE 中,BNN 适用于高维度的拓扑优化任务,结合生成模型生成的初始设计。BNN 通过强化学习优化拓扑设计,以实现多目标需求,如材料轻量化和结构强度提升。BNN 在处理非线性复杂结构中比高斯过程更具灵活性。条件贝叶斯优化(Conditional Bayesian Optimization, CBO)CBO 在贝叶斯优化中引入条件变量,以便在不同条件下优化结构。在 CAE 仿真中,CBO 适用于多目标条件下的拓扑优化。例如,结合生成模型生成的初始设计,CBO 可以根据不同载荷或材料条件对结构进行优化,确保生成的结构在不同条件下满足轻量化和强度需求。多目标贝叶斯优化(Multi-Objective Bayesian Optimization, MOBO)MOBO 扩展贝叶斯优化,使其能够同时优化多个目标。在 CAE 拓扑优化中,MOBO 可以平衡多个设计需求(如材料成本、轻量化、强度等)。结合生成模型和强化学习,MOBO 能够在高效探索设计空间的同时找到满足多目标的结构设计,是 CAE 多目标权衡的理想选择。顺序模型优化(Sequential Model-Based Optimization, SMBO)SMBO 通过逐步优化代理模型和评估样本点,实现高效的全局搜索。在 CAE 仿真中,SMBO 适合用于拓扑结构设计和多目标优化,尤其在生成模型生成的初始设计空间中逐步探索最优解。通过在采样点上不断优化,SMBO 能快速找到轻量化和强度平衡的最优拓扑结构。

贝叶斯优化与强化学习(Bayesian Optimization with Reinforcement Learning, BO-RL)BO-RL 结合贝叶斯优化和强化学习,用贝叶斯优化加速强化学习策略的优化。在 CAE 仿真中,BO-RL 可用于实时优化拓扑设计,通过强化学习控制结构生成过程,贝叶斯优化快速评估不同结构的适应度,以实现轻量化、强度等多目标需求。BO-RL 适用于需要快速迭代的拓扑优化场景。异常检测贝叶斯优化(Bayesian Optimization with Anomaly Detection, BO-AD)BO-AD 引入异常检测以避免探索劣质设计点,从而提高优化效率。在 CAE 中,BO-AD 可以过滤掉低质量的结构设计,帮助生成模型生成的结构快速接近最佳解。该架构适合用于拓扑优化过程中,快速聚焦于满足多目标需求的候选设计方案,加速轻量化和强度优化过程。层级贝叶斯优化(Hierarchical Bayesian Optimization, HBO)HBO 在多层级结构中执行贝叶斯优化,适合需要分层优化的复杂设计问题。在多尺度 CAE 仿真中,HBO 可用于多层级拓扑结构优化,如在宏观结构上优化轻量化,在微观结构上优化强度分布。结合生成模型,HBO 能够在多尺度设计中实现高效的多目标优化。
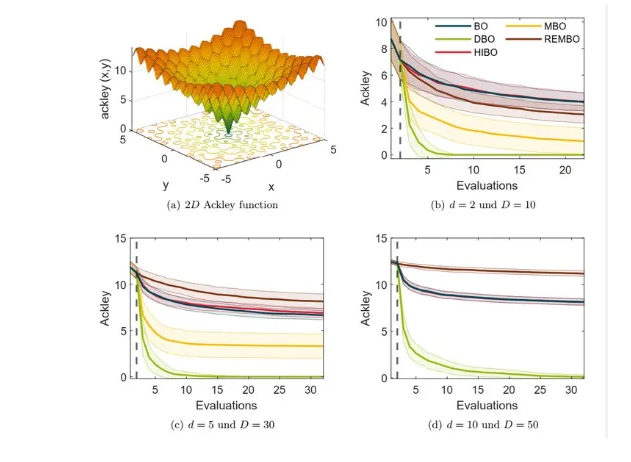
贝叶斯优化结合生成模型,为CAE仿真中的拓扑优化带来了全新的思路和工具。从高斯过程到层级贝叶斯优化,这些方法能够应对高维复杂设计空间、多目标权衡以及动态优化需求。通过与强化学习、异常检测等技术的融合,贝叶斯优化正成为解决复杂工程设计问题的理想选择,为实现轻量化与强度平衡提供了高效的路径。