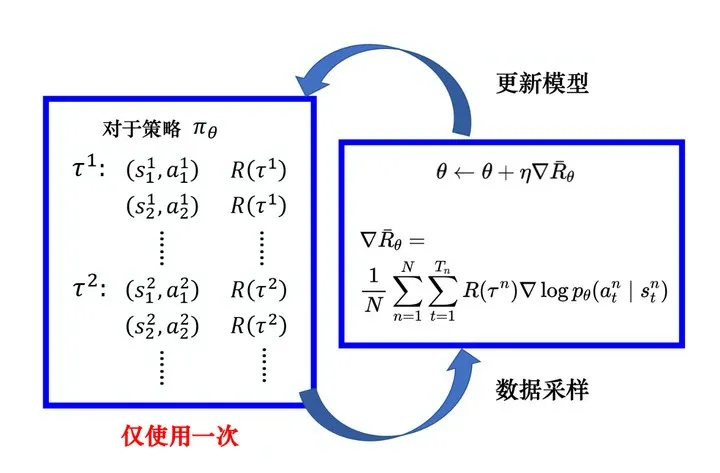
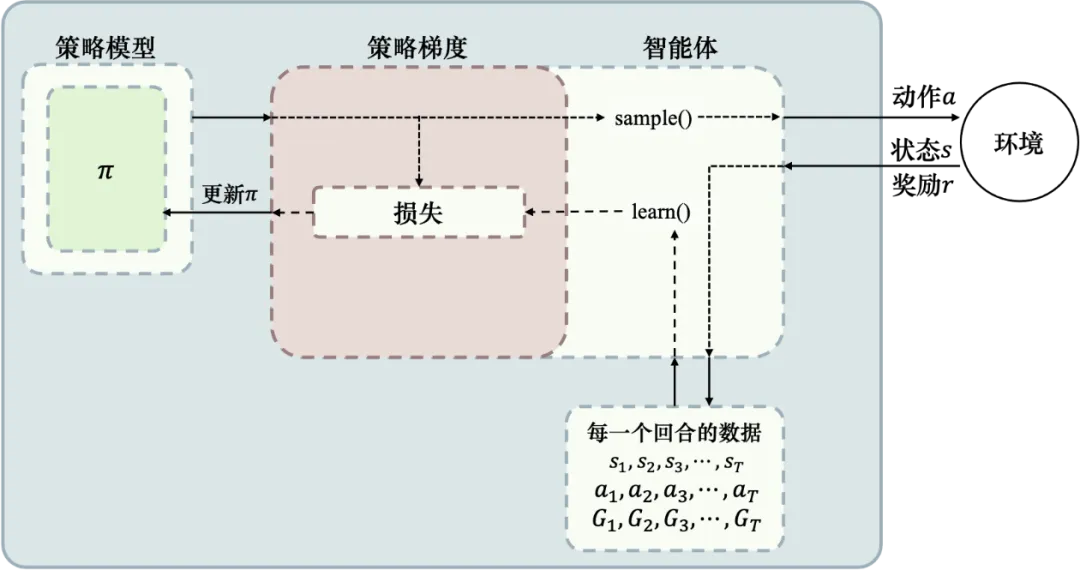
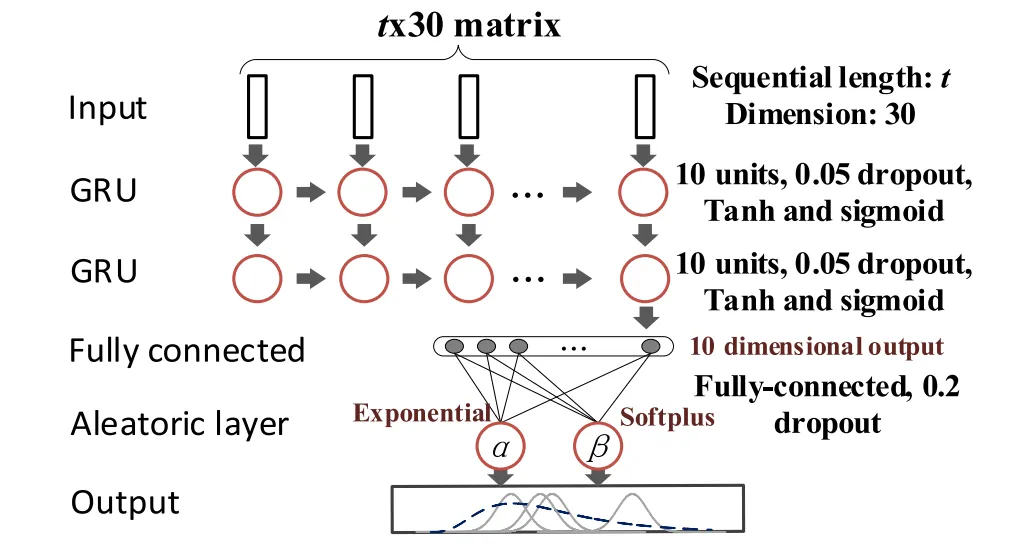
在材料科学与工程优化领域,智能算法的引入极大地提升了材料设计的效率和精度。强化学习(RL)和贝叶斯优化(BO)作为两大先进算法,能够高效探索材料组合、优化微观结构,并提升材料力学性能。本文将介绍多种强化学习方法及贝叶斯优化策略,探讨它们在材料与结构智能选择中的应用,为高性能材料的自动化筛选和优化提供新思路。
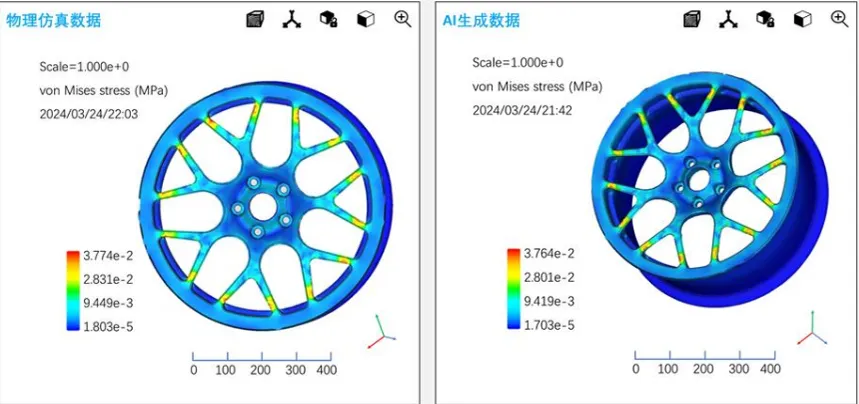
深度 Q 网络(Deep Q-Network, DQN):DQN 使用神经网络逼近 Q 值函数,适合离散动作空间中的策略优化。在材料设计中,DQN 可以通过不断尝试不同的材料组合和微观结构,学习哪些组合在力学性能上表现最佳。DQN 能够有效探索材料设计空间,并通过学习得到高效的材料组合策略。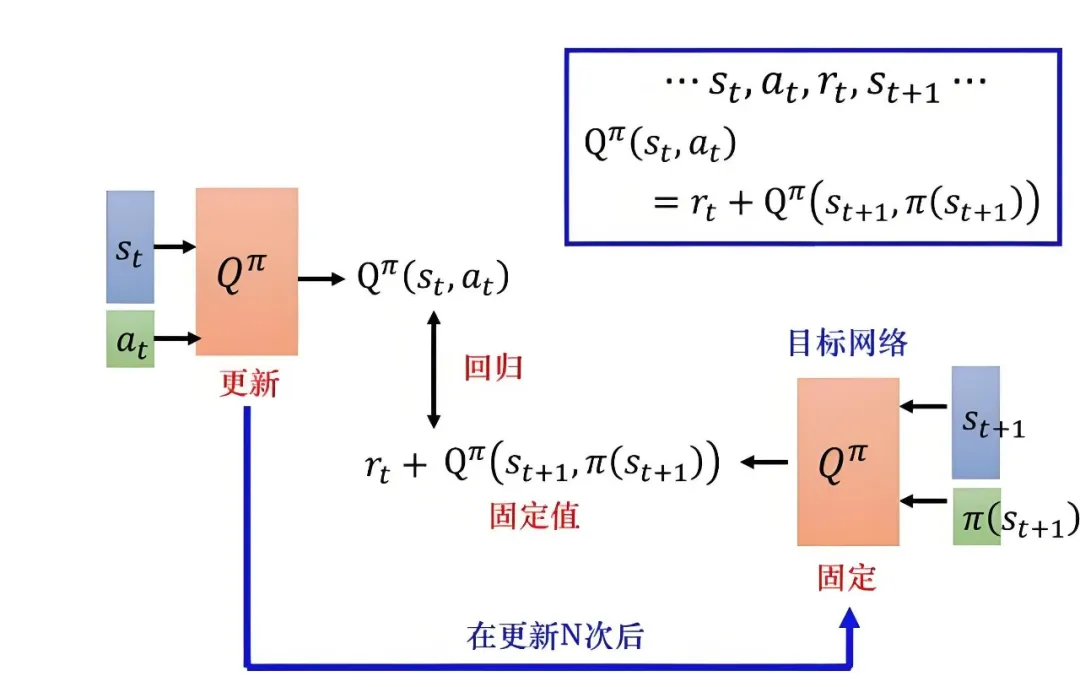
深度确定性策略梯度算法(Deep Deterministic Policy Gradient, DDPG):DDPG 适用于连续动作空间,结合策略网络和 Q 网络实现高效训练。在材料微观结构优化中,DDPG 可以帮助调节连续参数(如成分比例、晶体取向),使材料组合的力学性能最优。适用于复杂、连续的材料设计任务,帮助找到性能优异的材料组合。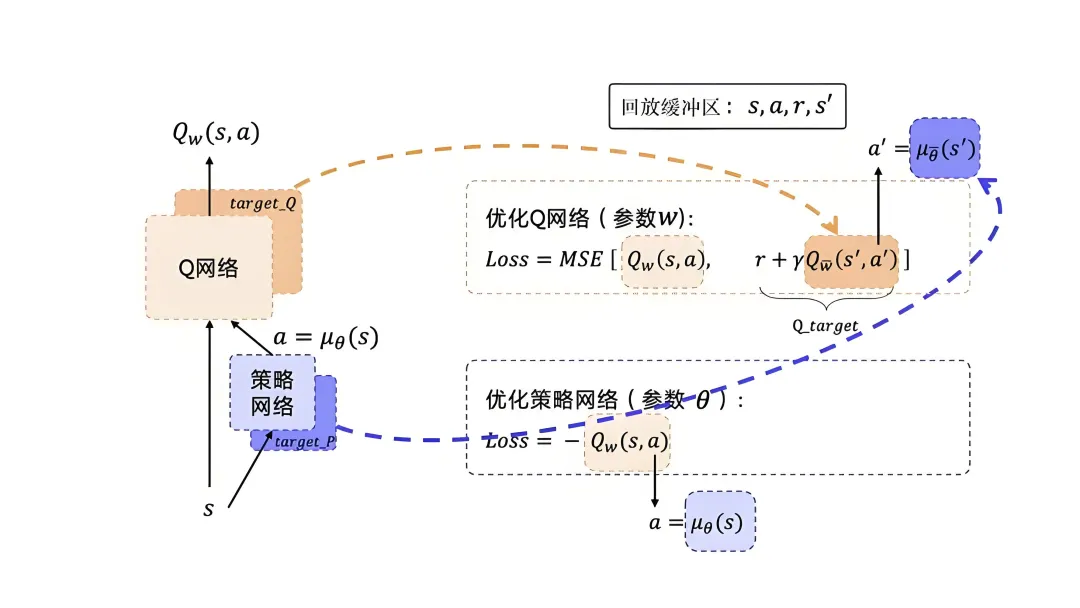
近端策略优化(Proximal Policy Optimization, PPO):PPO 通过限制策略更新幅度来提高训练的稳定性,适用于多目标优化任务。在材料设计中,PPO 可以优化材料组合中的多目标需求(如轻量化、强度、韧性),帮助探索不同设计方案的性能表现,找到多目标平衡的最优材料组合。
软策略梯度(Soft Actor-Critic, SAC):SAC 通过引入熵正则化提高策略探索性,适合不确定性环境。SAC 可以在材料设计中探索更广泛的设计空间,找到符合多目标需求的材料组合。它能处理不确定的微观结构特征,使材料在力学性能上表现出最佳状态,适合优化不确定性较高的材料设计问题。多智能体强化学习(Multi-Agent Reinforcement Learning, MARL):MARL 通过多个智能体的协同优化,适合处理复杂的多维设计任务。在材料组合优化中,每个智能体可以分别优化一个性能指标(如强度、延展性、耐腐蚀性等),通过协作找到符合多目标需求的材料组合。MARL 在多物理场和多特性优化中效果显著,适合高复杂度的材料设计。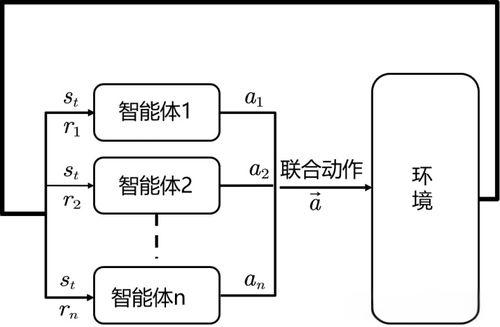
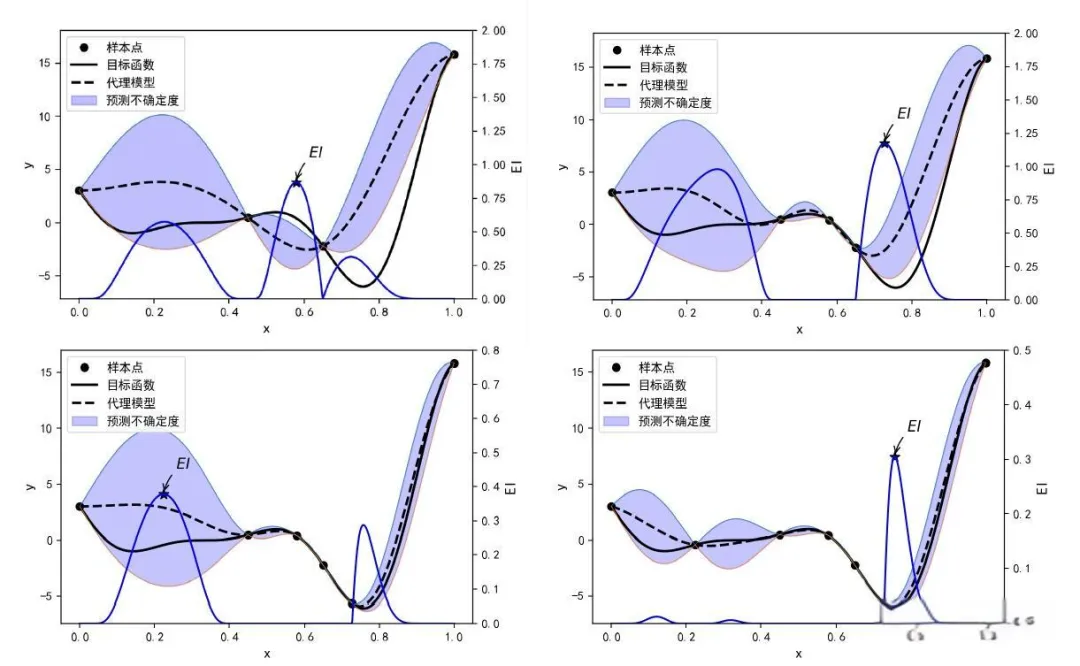
策略梯度方法(Policy Gradient Methods):策略梯度直接优化策略,适合处理连续和复杂的动作空间。在材料设计任务中,策略梯度方法可以直接优化材料组合策略,使组合在多目标约束下实现最优。适用于需要动态调整的材料设计方案,可以为 CAE 提供具有最佳性能的材料组合。高斯过程贝叶斯优化(Gaussian Process Bayesian Optimization, GPBO):GPBO 使用高斯过程构建代理模型,能够在高维空间中进行有效探索。在材料设计中,GPBO 可以利用历史实验数据预测材料组合的力学性能,并找到性能最优的设计组合。GPBO 适合优化复杂材料的多维特征参数,提供高效的材料组合推荐。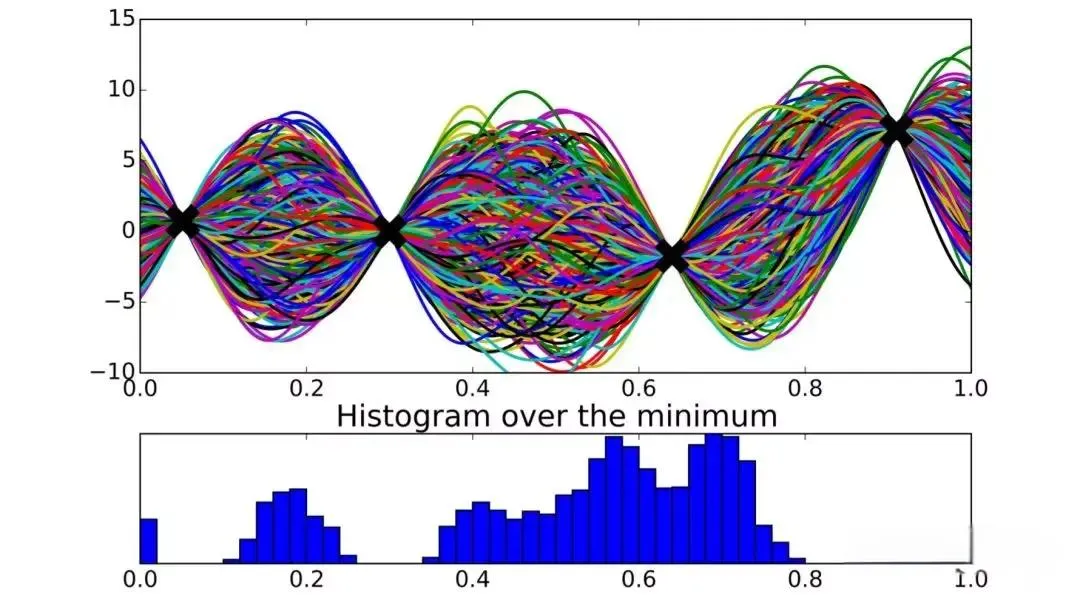
贝叶斯优化与梯度增强(Bayesian Optimization with Gradient Boosting, BO-GB):BO-GB将贝叶斯优化与梯度提升结合,提高优化效率。BO-GB 可以在材料设计中快速探索不同的微观结构组合,并利用梯度提升提高性能预测的精度。适合需要在较短时间内找到材料组合的场景,如 CAE 中的轻量化和强度优化。基于树结构的贝叶斯优化(Tree-Structured Parzen Estimator, TPE):TPE 是一种非参数贝叶斯优化方法,适合不规则搜索空间。在材料设计任务中,TPE 可以探索不规则的材料特性空间,找到满足力学性能需求的最佳组合。TPE 在异构材料或复杂结构的 CAE 优化中表现出色,能推荐具有多种性能优势的材料。
基于不确定性采样的贝叶斯优化(Uncertainty Sampling Bayesian Optimization, USBO):USBO 通过在高不确定性区域采样,提高探索效率。USBO 适用于材料微观结构和力学性能关系的优化。它可以通过聚焦于不确定性高的组合找到潜在的性能优异材料,支持多样化和创新材料组合的推荐。多目标贝叶斯优化(Multi-Objective Bayesian Optimization, MOBO):MOBO 通过同时优化多个目标,使其在多目标权衡中表现出色。MOBO 适合在材料设计中平衡多种性能需求(如强度、延展性、成本),并推荐符合 CAE 分析需求的材料组合。MOBO 能够在高维空间中平衡多目标性能,是精准材料设计的理想选择。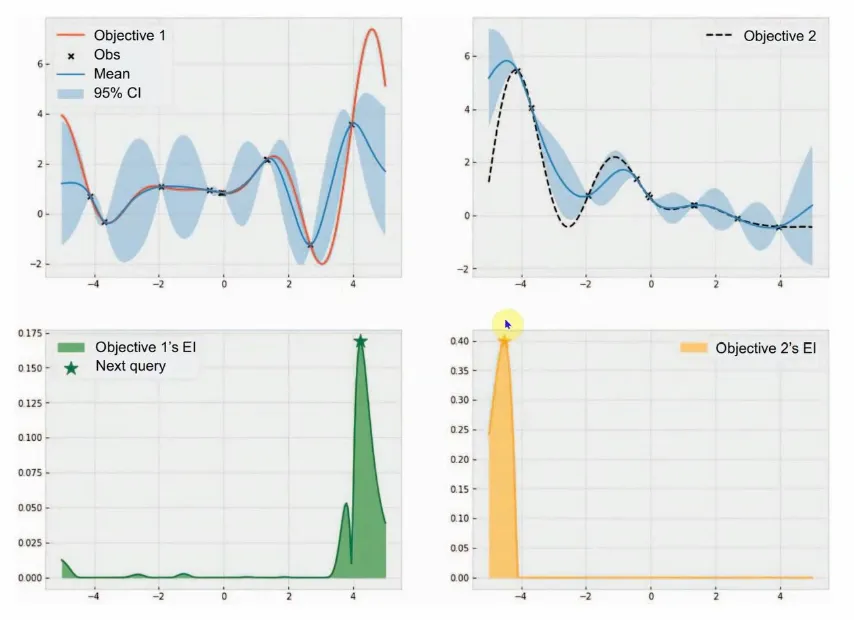
贝叶斯优化与强化学习结合(Bayesian Optimization with Reinforcement Learning, BO-RL):BO-RL 使用贝叶斯优化来调整强化学习策略的参数,使策略更加精准。在材料设计中,BO-RL 可以用于动态调整材料特性组合,通过强化学习策略找到最优材料组合,同时在贝叶斯优化的支持下快速收敛。适合高维复杂材料的探索与优化。、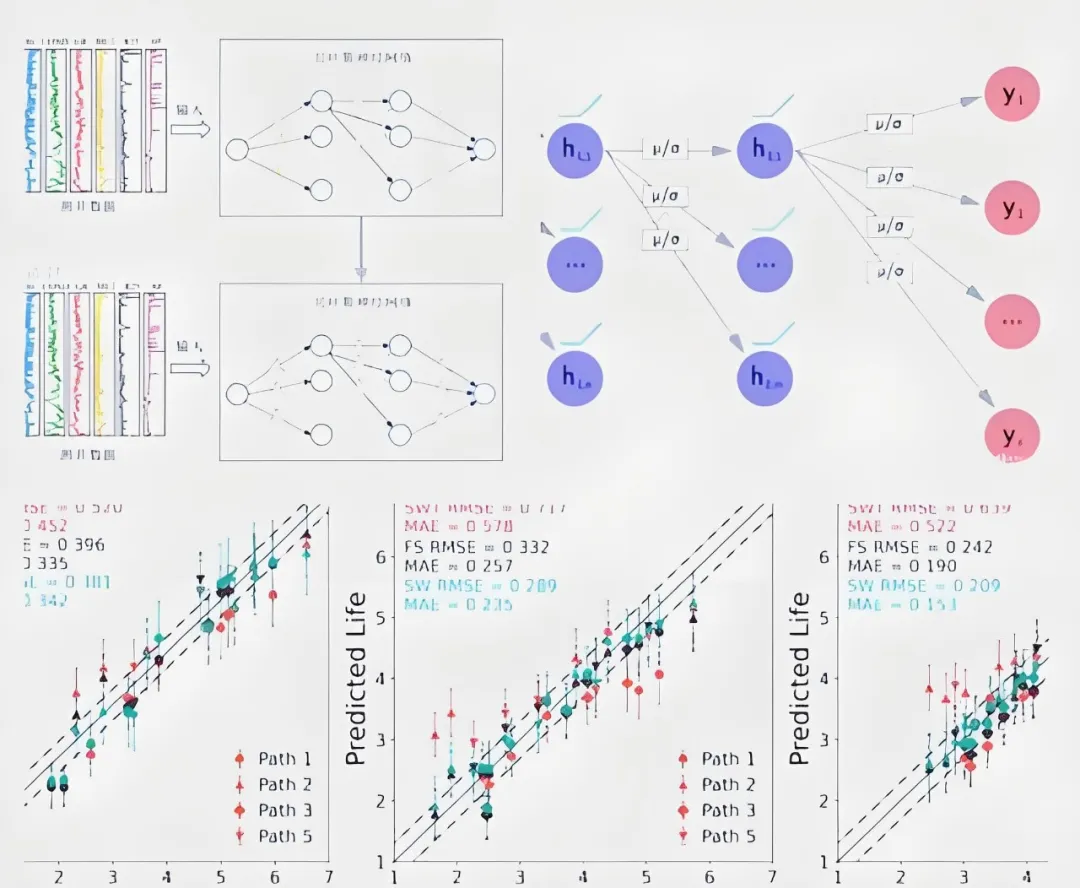
条件贝叶斯优化(Conditional Bayesian Optimization, CBO):CBO 在贝叶斯优化中引入条件变量,使得优化能够在特定条件下执行。在 CAE 材料设计中,CBO 可以根据不同的环境或物理条件(如温度、载荷)优化材料组合,使材料能够在各种条件下表现出优异性能。适合复杂材料设计任务中的多条件优化。强化学习与贝叶斯优化为材料智能选择提供了高效、精准的计算工具。从离散到连续,从单目标到多目标优化,这些方法能够在材料组合、微观结构设计及多物理场优化中发挥重要作用。未来,结合计算机辅助工程(CAE)与实验数据,这些智能优化方法将进一步推动新材料的研发和应用,加速材料科学的创新发展。